フラグメント分子軌道法（FMO法）
（アップロード ： 2010年5月24日）
ここでは、これまで使用したPPTなどを使ってフラグメント分子軌道法に関して説明します。量子化学の専門家だけがここを見るわけではないので、できるだけ専門知識が無い人にも分かるように説明にしたいと思います。
01
最初に、巨大系の量子化学計算に関する一般的な話をしましょう。量子化学計算とは分子中の電子のシュレーディンガー方程式を解くための計算方法で、現在、小さな分子に関しては非常に高精度な解を得ることができます。しかし、量子化学計算では、計算コストが、系のサイズ（系の原子数）の増加に対してN4以上で増大することが知られています。

具体的にどういうことかというと . . .

今、水分子を1秒で計算できる手法があるとします。この方法を現実の生体分子（例えばプリオンタンパク複合体）に適用した場合、どのくらいの時間が掛かるでしょうか？プリオンタンパク複合体は水分子と比較すると、原子数は約576倍です。仮に、原子数の増加に対して計算コストがN3で増大するとしても、以下に示す通り、6年以上の計算時間が必要となります。これでは、決して実用的とはいえません。従って、低分子を取り扱うのと同様のやり方でタンパク質などの巨大分子を扱うのは不可能で、なんらかの新しい手法を考える必要が出てきます。

そこで、フラグメント分子軌道法（FMO法）です。
02
フラグメント分子軌道（FMO）法 [1] は、1999年に北浦先生により提案された手法です。FMO法では、系全体を比較的小さなフラグメントに分割し、ラグメント単体（モノマー）およびフラグメントペア（ダイマー）の計算のみから、全体のプロパティを算出します。従って、小さな計算を複数回実行するだけでよく、計算コストを大きく減らすことが可能となります。そして、モノマーやダイマーの計算が独立しているので、高い並列効率が実現されます。また、全エネルギーの定式化の中で、フラグメント間相互作用エネルギー（IFIE）[2] が定義され、分子間相互作用の解析などにおいて有効に利用できることが知られています。以下、FMO法を用いた計算の手続きに関して説明します。
03
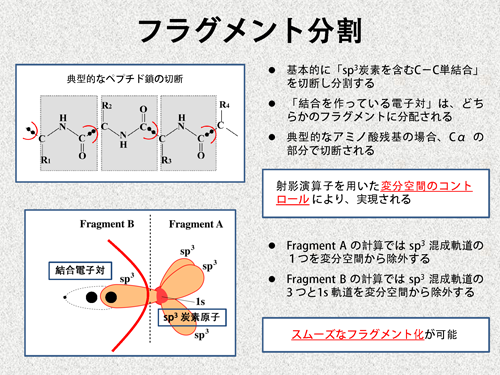
タンパク質のような巨大分子のFMO計算を行う場合、共有結合を切断するようなフラグメント分割を行う必要があります。ここでは、まず、結合の切断を伴うフラグメント分割がどのように行われるかを説明します。

通常、共有結合を切断するようなフラグメント分割を行う場合、SP3炭素原子の箇所で切断します（一般的に、このような原子のことをBDAと呼びます）。例えば、典型的なペプチド鎖の場合、下図のように、α炭素の部分で切断されることになります。この時、結合を形成している電子対は、切断部のSP3炭素原子ではない方のフラグメントに分配されます。実際の計算では、このような結合の切断は、射影演算子を用いた変分空間のコントロールによって実現されます。少し専門的になりますが、もう少し詳しく見てみましょう。

例えば、下図のように、フラグメントA（以下A）とフラグメントB（以下B）に分割する場合を考えます。切断部位のSP3炭素原子はAに含まれているので、結合の電子対はBに分配されます。よって、SP3混成軌道の1つはBの計算で占有されることになり、Aの計算では、この軌道が占有されないようにする必要があります。そこで、Aの計算を行う際、射影演算子を使ってこの軌道を変分空間から除外します。一方、Bの計算では、結合の電子対が占有する軌道を作るため、SP3炭素上の基底関数を含めて計算を行います。しかし、この基底関数には、既にAの計算で占有されている4つの軌道（1s軌道と3つのSP3軌道）が含まれています。従って、Bの計算では、これらの軌道が占有されないように、射影演算子を使って変分空間から除外します。

このように、射影演算子を用いることで、結合の切断を伴うフラグメント分割がスムーズに実現されます。
04
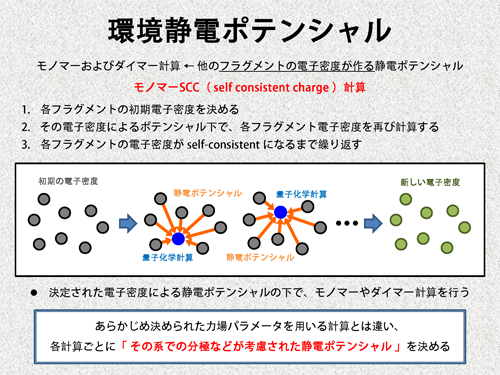
FMO法では、フラグメントのモノマーおよびダイマー計算から、全体のプロパティを算出しますが、この際、周囲のフラグメントの電子密度が作る静電ポテンシャルを考慮して計算を行います。よって、モノマーやダイマー計算を実行する前に、各フラグメントの電子密度を決めておく必要があります。これを決める計算のことを、モノマーSCC（monomer self consistent charge）計算と呼びます。

モノマーSCC計算では、まず最初に、各フラグメントの初期電子密度を適当に決めます。次に、この初期電子密度による静電ポテンシャルの存在下で、各フラグメントのモノマー計算を行います。全てのフラグメントに関して計算が終わると、先ほどの初期密度とは異なる新しい電子密度が得られています。そこで、今度は、この新しい電子密度を初期電子密度と考えて、同じように計算を行います。これを、自己無矛盾な電子密度になるまで繰り返し、最終的な電子密度とします。そして、この最終的な電子密度が作る静電ポテンシャル（我々は環境静電ポテンシャルと呼んでいます）を考慮して、モノマー計算やダイマー計算を実行します。

ここで示したように、FMO法では、計算ごとに適切な静電ポテンシャル決め、モノマー計算やダイマー計算を行います。従って、この点において、経験ポテンシャルを用いる他の手法と大きく異なると言えます。
05
最後に、環境静電ポテンシャルの影響を考慮したモノマー計算とダイマーの計算の結果から、全体のプロパティが算出されます。

例えば、全エネルギーは、下図の1つ目の式から計算されます（モノマーとダイマーのエネルギーのみから計算されていることに注意してください）。量子化学計算で最もよく使用されるハートリ−・フォック（HF）法の場合、この式は、2つ目の式のように書き換えることができます。ここで、ダッシュがついたエネルギーは、環境静電ポテンシャルの寄与を取り除いたモノマーのエネルギーです。つまり、第1項目は、各フラグメントの内部エネルギーの和になっています。全体のエネルギーが、フラグメントの内部エネルギーの和と第2項で記述されているので、この第2項はフラグメント間の相互作用エネルギーであると考えることができます。そこで、第2項の値を、IFIE（Inter Fragment Interaction Energy）もしくはPIE（Pair Interaction Energy）と定義し、生体分子などの相互作用解析に利用します。

また、HF計算に加え、MP2計算 [3][4][5] を実行することで、van der Waals相互作用を考慮した結果を得ることもできます。
ここまで、FMO法のアウトラインを解説してきましたが、不十分な部分もあるかと思います。今後、できるだけアップデートし、わかりやすい解説にしていきたいと思います。
refrence
[1] Fragment molecular orbital method: an approximate computational method for large molecules,K. Kitaura, E. Ikeo, T. Asada, T. Nakano, and M. Uebayasi,Chem. Phys. Lett., 313 (1999) 701-706 (DOI: 10.1016/S0009-2614(99)00874-X)
[2] Fragment molecular orbital method: use of approximate electrostatic potential, T. Nakano, T. Kaminuma, T. Sato, K. Fukuzawa, Y. Akiyama, M. Uebayasi, and K. Kitaura, Chem. Phys. Lett., 351 (2002) 475-480 (DOI: 10.1016/S0009-2614(01)01416-6)
[3] A parallelized integral-direct second-order Moller-Plesset perturbation theory method with a fragment molecular orbital scheme, Y.Mochizuki, T. Nakano, S. Koikegami, S. Tanimori, Y. Abe, U. Nagashima, and K. Kitaura, Theor. Chem. Acc., 112 (2004) 442-452 (DOI: 10.1007/s00214-004-0602-3)
[4] Large scale MP2 calculations with fragment molecular orbital scheme, Y. Mochizuki, S. Koikegami, T. Nakano, S. Amari, K. Kitaura, Chem. Phys. Lett., 396 (2004) 473-479 (DOI: 10.1016/j.cplett.2004.08.082)
[5] Second order Moller-Plesset perturbation theory based upon the fragment molecular orbital method, D. G. Fedorov and K. Kitaura, J. Chem. Phys., 121 (2004) 2483-2490 (DOI: 10.1063/1.1769362)