| Japanese top page / English top page |
PAICS
Parallelized ab initio Calculation System based on FMO
|
fragment molecular orbital method |
|||
|
| |||
| In this page, we give a brief description about the fragment molecular orbital (FMO) method using PPTs, which have been used in the previous presentations. | |||
|
First, we discuss difficulty of quantum chemical treatments of large molecules including biomolecular systems. In quantum chemistry, we perform calculations for solving the Schrodinger equation of electrons. Today, we can obtain the solution with a very high accuracy for small size molecules or middle size molecules. However, in general methods of quantum chemistry, the computational time is known to increase with more than N4 of a target molecular size.
For example, we consider a quantum chemical method that can complete the calculation of a water molecule in just one second. In the case using this method for real biomolecualr systems, how long does it take to complete the calculations? The following molecule is a complex of prion protein with a small molecule, and this system contains 1729 atoms. The number of atoms increases by about 576 times. Even if we assume that the computational time increases with N3 of the system size, the calculation of this molecule requires more than 6 years. This simple consideration clearly shows that we cannot perform quantum chemical calculations of biomolecular systems actually with the conventional method used for small size molecules or middle size molecules. So, new methods are required for quantum chemical treatment of biomolecular systems. |
|||
 |
|||
|
Fragment molecular orbital method (FMO) [1] is one of the most efficient approaches for quantum chemical calculations of large molecules. In the FMO method, a target molecule is divided into small fragments. For example, in the case of protein, amino acid residue is treated as a single fragment. The total property can be evaluated only from the calculations of the fragments and pairs of fragments. In the FMO method, we refer to the fragment as "monomer" and to the pair of fragments as "dimer".
This feature of the FMO method leads some computational advantages. One of them, only small calculation is needed for evaluation of total properties, in which monomer or dimer calculation is completely independent of each other. It means high applicability for parallel computing of the FMO method. The FMO method provides not only computational advantage but also a very useful quantity, which is inter fragment interaction energy (IFIE) [2]. In the case of biomoleular system, each residue is treated as single fragment. Thus, by using the IFIE, we can obtain the detailed information about interaction energy, for example, interaction between two residues or between residue and ligand. In the following PPTs, I'll explain more details of the FMO scheme. |
|||
 |
|||
|
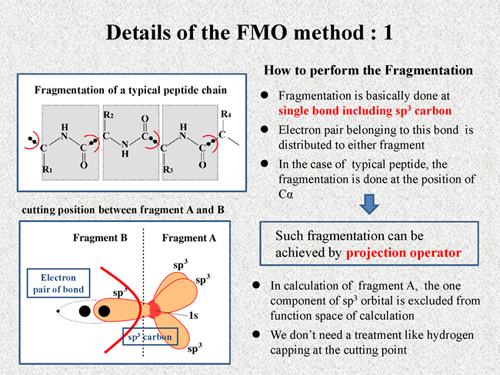
First, I explain how to perform the fragmentation in FMO method. Fragmentation is basically done at single bond including sp3 carbon. And electron pair belonging to this bond is distributed to either fragment. Consequently, in the case of a typical peptide, the fragmentation is done at the position of Cα as shown in this figure.
In actual calculation, such fragmentation can be achieved by projection operator. It is one of familiar techniques of quantum chemistry. Here, I briefly explain about the usage of the projection operator. This figure shows a cutting point between fragment A and fragment B. The fragmentation is done at a single bond including sp3 carbon, and a electron pair is distributed into fragment B. In calculation of fragment A, one component of sp3 orbital in fragment B is excluded from the function space. On the other hand, in calculation of the fragment B, three component of sp3 orbital and one component of 1s orbital are excluded from the function space. Like this, we can achieve the fragmentation very naturally in the FMO method. Thus, we don't need a treatment like hydrogen capping at the cutting point. |
|||
 |
|||
|
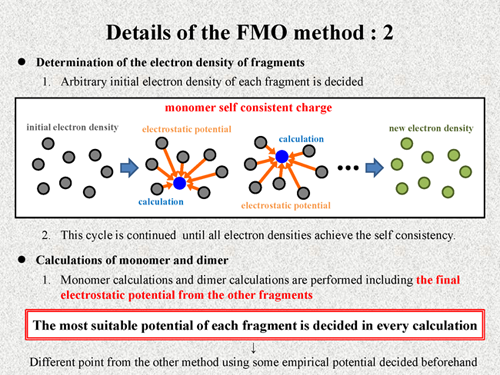
Next, I show the process of the FMO calculation. At start of calculation, arbitrary initial electron densities of each fragment are decided, and quantum chemical calculation is performed for each fragment including electrostatic potential from the other fragments. By these calculations, new electron densities of all fragments are decided. We consider that this calculation is one cycle, and such a cycle is continued until all electron densities achieve the self consistency. This procedure is called "monomer self consistent charge" (monomer SCC) process.
After this procedure, monomer calculations and dimer calculations are performed including the final electrostatic potential from the other fragment. Thus, in the FMO method, the most suitable potential of each fragment is decided in every calculation. It is a very different point from the other method using some empirical potential which are decided beforehand. |
|||
 |
|||
|
Using the results of the monomer calculations and the dimer calculations, the total properties are evaluated. For example, the total energy of the system is calculated by the following equation. EI is monomer energy of the fragment I and EIJ is dimer energy of the fragment I and J. As shown in this equation, the total energy is approximately calculated by using only monomer and dimer energies. Here, N is the number of the fragments.
The total energy can be rewritten into the following equation [2]. In this equation, E' is the monomer energy of fragment I, from which the contribution of the electrostatic potential from the other fragments is excluded, that is to say, this E' is just internal energy of the monomer. Thus, another term of this equation is naturally considered to be interaction energy between fragments. Thus, this ΔEIJ is the IFIE of the FMO method. These values are calculated in actual FMO calculations and utilized for our interaction analysis. Normally, MP2 calculations are additionally performed to evaluate dispersion interaction or van der Waals interaction [3][4][5]. |
|||
 |
|||
| [1] | Fragment molecular orbital method: an approximate computational method for large molecules,K. Kitaura, E. Ikeo, T. Asada, T. Nakano, and M. Uebayasi,Chem. Phys. Lett., 313 (1999) 701-706 (DOI: 10.1016/S0009-2614(99)00874-X) | ||
| [2] | Fragment molecular orbital method: use of approximate electrostatic potential, T. Nakano, T. Kaminuma, T. Sato, K. Fukuzawa, Y. Akiyama, M. Uebayasi, and K. Kitaura, Chem. Phys. Lett., 351 (2002) 475-480 (DOI: 10.1016/S0009-2614(01)01416-6) | ||
| [3] | A parallelized integral-direct second-order Moller-Plesset perturbation theory method with a fragment molecular orbital scheme, Y.Mochizuki, T. Nakano, S. Koikegami, S. Tanimori, Y. Abe, U. Nagashima, and K. Kitaura, Theor. Chem. Acc., 112 (2004) 442-452 (DOI: 10.1007/s00214-004-0602-3) | ||
| [4] | Large scale MP2 calculations with fragment molecular orbital scheme, Y. Mochizuki, S. Koikegami, T. Nakano, S. Amari, K. Kitaura, Chem. Phys. Lett., 396 (2004) 473-479 (DOI: 10.1016/j.cplett.2004.08.082) | ||
| [5] | Second order Moller-Plesset perturbation theory based upon the fragment molecular orbital method, D. G. Fedorov and K. Kitaura, J. Chem. Phys., 121 (2004) 2483-2490 (DOI: 10.1063/1.1769362) | ||
|