FMO法による生体分子の相互作用解析の高速化
（ アップロード : 2010年5月17日 ）
タンパク−リガンド間の相互作用エネルギーを高速に得るために行った工夫を、プレゼンの資料などを用いてご紹介します。また、ここで紹介している計算は論文 [1] [2] として出版されておりますので、詳細はそちらを参照してください。
01
FMO法 [3] では、系全体をフラグメントに分割し、モノマーとダイマーの計算から全エネルギーを算出することで、計算コストを大幅に減少させることが可能となります。しかし、創薬でFMO計算を利用するには、さらなる高速化が必要です。そこで、「創薬に利用できる情報」を高速に得るということを、PAICS [4] の開発指針の一にしています。ここで、我々が考える創薬に利用できる情報とは、タンパク−リガンド間の相互作用もしくはタンパク−タンパク間の相互作用に関する情報です。つまり、具体的には、タンパク−リガンド間やタンパク−タンパク間のフラグメント間相互作用エネルギー（IFIE）[5] です。
02
生体分子ではvan der Waals相互作用が重要であることが知られています。従って、創薬にFMO計算を利用する場合、最低でも、MP2計算を行う必要があります。この時、計算時間の約7割がMP2計算に費やされます（下図）。従って、FMO計算の高速化のためには、まず最初に、MP2計算を高速化しなければなりません。そこで、我々は、RI-MP2法 [6] を採用しMP2計算の高速化を試みました。
03
RI-MP2法は、resolution of the identityという近似を使い、4中心積分を3中心積分で近似し、計算コストを大幅に削減する手法です。ここでは、理論や実装に関する詳細は省略しますが、興味がある方は論文 [1] を参照して下さい。
04
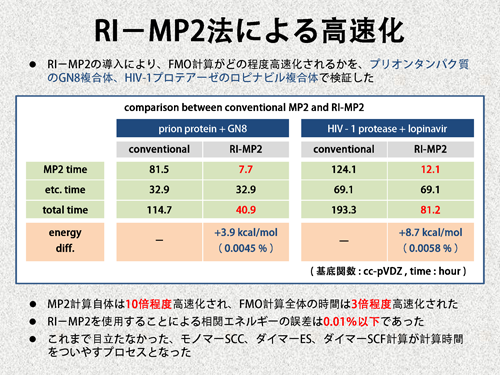
RI-MP2法の導入による高速化を確認するため、2つの実在する生体分子に関してテスト計算を行いました。これによると、MP2計算は約10倍、その結果、FMO計算は約3倍高速化されました。また、RI-MP2法の導入による全相関エネルギーの誤差は、0.01%以下でした。このように、MP2計算のコストを減らすことに成功しましたが、同時に、これまで目立たなかったダイマーSCF計算、モノマーSCC計算が多くの時間を占めるようになりました。
05
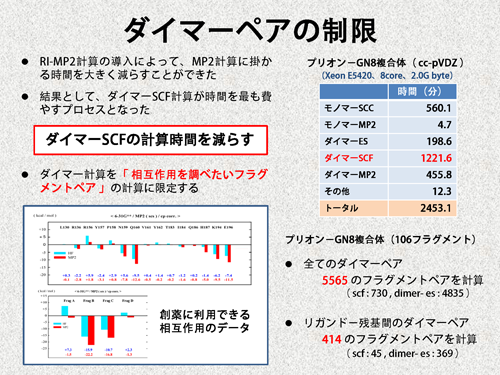
上で述べたように、ここでの目標は、創薬に利用できる情報を高速に得ることです。そして、我々は、タンパク−リガンド間やタンパク−タンパク間のIFIEを、創薬に利用できる情報と考えています。そこで、ダイマー計算を、これらのIFIEの計算に必要なフラグメントペアのみに限定しました。これだと、複合体の全エネルギーを得ることはできなくなりますが、目的としているIFIEを得ることはできます。プリオン−GN8複合体の場合、計算対象をタンパク−リガンド間のIFIEに限定すれば、必要なダイマー計算の数が5565から414に減少し、計算時間を大幅に減らすことが可能となります。
06
ダイマー計算の時間を減らすことができたので、今度は、モノマーSCC計算の時間を減らす工夫を考えました。まず、ダイナミックアップデートという手法を導入しました。これは、フラグメントの電子密度のアップデートに関する工夫ですが、詳細は論文 [2] を参照してください。次に、収束したタンパク部分の電子密度を次回の計算の初期密度として利用するようにしました。これは、特定のタンパクに対し、異なるリガンドの複合体を多数計算する場合に有効となります。
07
ここまで、タンパク−リガンド間やタンパク−タンパク間の相互作用の情報を高速に計算するために、RI-MP2法の導入、ダイマー計算の制限、ダイナミックアップデートの導入、収束済みの電子密度の利用といった工夫を行って来ました。その結果、プリオン−GN8複合体では、タンパク−リガンド間のIFIEに限定すれば、 FMO/RI-MP2/cc-pVDZ レベルの計算が8コアのみで4.3時間で完了できるるようになりました。例えば、我々の研究室には39ノードの計算機があり、これをフルに使用すれば、

24 / 4.3 * 39 = 218

となり、1日に218のリガンド分子に関する相互作用の情報 (IFIE) を得ることができるということになります。多数のリガンド分子に関して、網羅的にIFIE解析を行うことで、効果のある化合物と無い化合物の違いを調べたり、ドッキングシミュレーションのポテンシャルの改良などに利用できると期待しています。
多数の化合物に関してIFIEの解析を行う場合、PAICSは最適のプログラムだと思います。是非、ご利用ください。
refrence
[1] Fragment molecular orbital calculation with RI-MP2 method, T. Ishikawa and K. Kuwata, Chem. Phys. Lett., 474 (2009) 195-198 (DOI: 10.1016/j.cplett.2009.04.045)
[2] Acceleration of monomer self-consistent charge process in fragment molecular orbital method, T. Ishikawa and K. Kuwata, C.B.I.J., 10 (2010) 24-31 (DOI: 10.1273/cbij.10.24)
[3] Fragment molecular orbital method: an approximate computational method for large molecules, K. Kitaura, E. Ikeo, T. Asada, T. Nakano, and M. Uebayasi, Chem. Phys. Lett., 313 (1999) 701-706 (DOI: 10.1016/S0009-2614(99)00874-X)
[4] Theoretical study of the prion protein based on the fragment molecular orbital method, T. Ishikawa, T. Ishikura, and K. Kuwata, J. Comput. Chem., 30 (2009) 2594-2601 (DOI: 10.1002/jcc.21265)
[5] Fragment molecular orbital method: use of approximate electrostatic potential, T. Nakano, T. Kaminuma, T. Sato, K. Fukuzawa, Y. Akiyama, M. Uebayasi, and K. Kitaura, Chem. Phys. Lett., 351 (2002) 475-480 (DOI: 10.1016/S0009-2614(01)01416-6)
[6] Use of approximate integrals in ab initio theory. An application in MP2 energy calculations. M. Feyereisen and G. Fitzgerald,Chem. Phys. Lett., 208 (1993) 359-363 (DOI: 10.1016/0009-2614(93)87156-W)