正常型プリオンタンパク質の分子内相互作用解析
（ アップロード : 2010年10月05日 ）
正常型プリオンタンパク質に関して、残基−残基間相互作用および残基−溶媒分子間相互作用を解析した例を、これまでのプレゼンで使用した資料を用いて説明します。また、ここで紹介している計算は論文として出版されておりますので [1] 、詳細はそちらを参照して下さい。
01
通常、量子化学計算では、原子核の位置を固定し、電子の運動方程式（シュレーディンガー方程式）を解きます。よって、量子化学計算でタンパク質の構造変化を直接シミュレーションすることは困難です。しかし、プリオン病の原因は正常型から異常型へのコンフォーメーション変化なので、この構造変化のプロセスを調べることは重要な研究課題です。そこで、コンフォーメーション変化に関連する情報を得るために、正常型プリオンタンパク質に関してFMO計算 [2] を実行しました。

具体的には、正常型プリオンタンパク質に溶媒分子加えたモデル系を作成し、FMO計算を実行し、残基−残基間相互作用エネルギーと残基−溶媒分子間相互作用エネルギーを、フラグメント間相互作用エネルギー（IFIE） [3] から算出しました。これらを解析することで、正常型の構造維持に重要に寄与する相互作用を特定し、異常型へのコンフォーメーション変化に関連する情報を得ようと試みました。
02
まず、PDBを初期構造とし、古典的な分子動力学計算のトラジェクトリーからランダムに40点の構造を抜き出しました。そこから8Å以上離れた溶媒分子を取り除きモデル構造（下図参照）とし、これらに関してFMO計算を実行し、残基−残基間相互作用および残基−溶媒間相互作用の解析を行いました。計算にはRI-MP2法を用い、基底関数にはcc-pVDZを使いました。
03
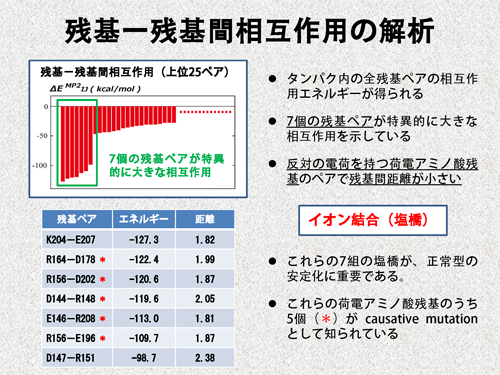
それでは、計算結果を見てみましょう。最初に、残基−残基間相互作用エネルギーを解析します。以下のグラフには、最も相互作用エネルギーが大きかった25組の残基ペアのエネルギーがプロットされています。これを見ると、7組のペアが特異的に大きな相互作用エネルギーを示していることが分かります。そして、これらのペアは、互いに反対の電荷を持った荷電アミノ酸残基であり、残基間距離も非常に小さいことが分かります（表を参照）。従って、イオン結合（塩橋）を形成していると考えられ、この7組の塩橋が正常型プリオンタンパク質の安定化に重要に寄与していると推測できます。また、7組のうち5組の塩橋を形成する残基は、病原性のミューテーション（病気が起こりやすくなるミューテーション）として知られており、これらの塩橋が正常型の安定化に重要であるこという推測と矛盾しません。
04
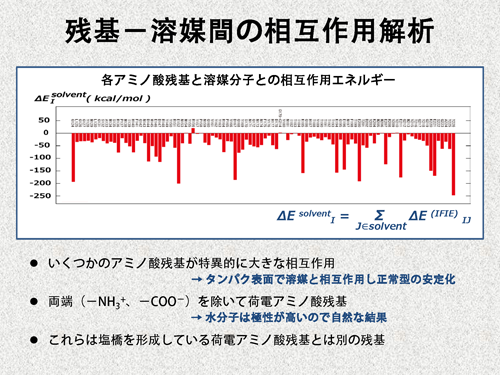
次に、残基−溶媒分子間相互作用エネルギーに注目します。いくつかのアミノ酸残基が溶媒分子と特異的に大きな相互作用エネルギーを示していることが分かります。これらの残基は、溶媒分子と相互作用することで、正常型の構造維持に寄与していると考えられます。詳しく見てみると、両末端の残基を除き、全て荷電アミノ酸残基であることが分かります（両末端は終端処理として電荷を持っている）。これは、水分子が高い極性をもっているため当然の結果といえます。

ここで重要なのは、溶媒分子と大きな相互作用エネルギーを稼いでる荷電アミノ酸残基は、塩橋を形成している荷電アミノ酸残基とは別の残基であるということです。つまり、荷電アミノ酸残基は、「塩橋を形成する役割」か「溶媒と相互作用する役割」のどちらか一方を通じて、正常型の構造維持に寄与しているということになります。今回の例では、22個の荷電アミノ酸残基のうち、13個が塩橋を形成し、残りの9個が溶媒分子と強く相互作用していました。そして、これらの違いは、計算された相互作用エネルギーから明確に区別できました。

ここで少し一般的な議論をすると . . .

タンパク質は、エネルギー的に最も有利な構造をネイティブ構造として選択しているはずです。例えば、今回の正常型プリオンタンパク質では、K204とE207が塩橋を形成していました（上の表参照）。しかし、これらが塩橋を作らず、タンパク表面に突き出て溶媒と相互作用するような構造も、タンパクのコンフォーメーション空間には多数存在するはずです。それでも、K204とE207が塩橋を形成する構造がネイティブ構造なのは、 その構造がエネルギー的に最も有利だからです。つまり、K204やE207が、溶媒分子と相互作用する役割ではなく塩橋を形成する役割を持っているのには、エネルギー的な必然性があるからです。

ここでは、正常型プリオンタンパク質の荷電アミノ酸残基のみに注目しましたが、様々なタンパク質に関して、「各残基がネイティブ構造の安定化に果たす役割」を網羅的に調べることができれば、タンパク質の高次構造形成のメカニズムに関連する面白い研究ができるのではないかと思います。もちろん、高次構造の形成にはエントロピー的な効果も重要で、相互作用エネルギー（つまり、エンタルピー的な効果）だけで全が理解できるとは思いません。が、FMO法を応用する可能性の1つであると思います。
05
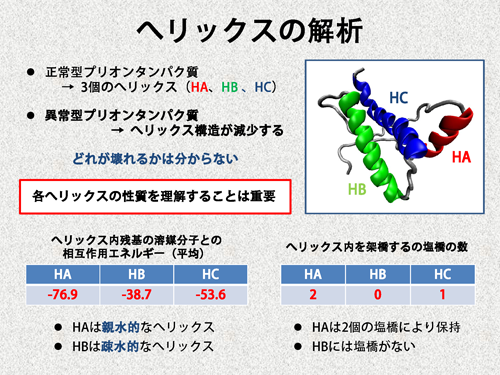
今度は、各へリックスごとに相互作用を見てみましょう。正常型プリオンタンパク質には3つのへリックスが存在します（AH、HB、HC）。そして、異常型へ変化すると、へリックス構造の一部が消失することが知られています。しかし、どのへリックス構造が壊れるのかは分かっておらず、それを突き止めることができれば、プリオン研究における大きな進展となります。もちろん、正常型プリオンタンパク質の量子化学計算のみから、壊れるへリックスを予測することはできませんが、「各へリックスの性質」を議論することは可能です。

例えば、各へリックスに含まれるアミノ酸残基の溶媒分子との相互作用エネルギーの平均値は、HAが最も大きくHBが最も小さくなりました（表を参照）。従って、HAは親水的性質を持ったへリックスであり、HBは疎水的性質を持ったへリックスであると言えます。また、今回の計算で特定された7個の塩橋のうち、2個がHA内に存在するのに対して、HBにはそのような塩橋が存在しません。従って、HAのへリックス構造はイオン的な相互作用により強固に保たれている一方で、HBのへリックス構造はイオン結合という意味では弱いと推測できます。
06
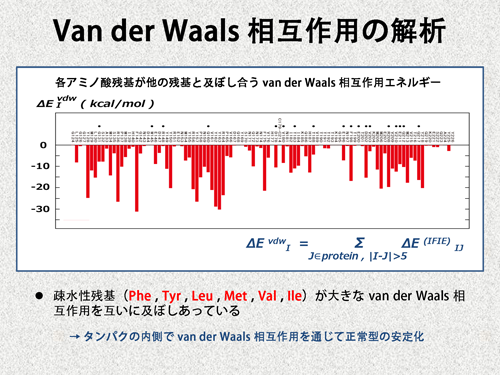
次は、van der Waals 相互作用に注目します。量子化学計算では、van der Waals 相互作用は電子相関として個別に計算されるので、van der Waals 相互作用だけを抜き出した解析が可能となります。以下に示したのは、各アミノ酸残基が自分以外のアミノ酸残基と及ぼすvan der Waals 相互作用エネルギーです。これを見ると、疎水性残基が比較的大きな相互作用を示していることが分かります。これは、タンパク質科学の一般的な考え方、つまり、「親水性残基はタンパク表面で溶媒分子と相互作用し、疎水性残基は内側で互いに非極性の相互作用をして、タンパク質の立体構造に寄与する」という見解と、矛盾しない結果だといえます。
07
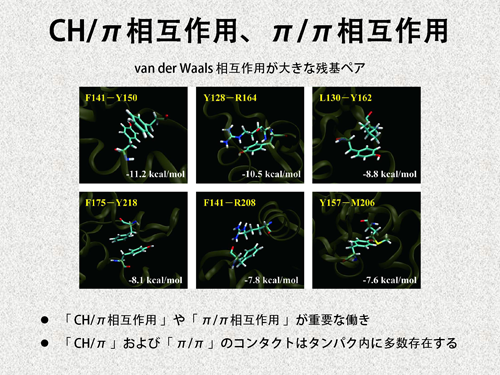
近年、CH/π相互作用やπ/π相互作用が、化学の様々な場面で重要な役割を果たしていると考えられています。以下に、我々の計算で最も van der Waals 相互作用を稼いでいた6個の残基ペアを示します。これらのペアは全てCH/πもしくはπ/π相互作用を及ぼしあっています。また、ここに示したもの以外にも、数多くのCH/πやπ/πコンタクトが高い相互作用エネルギーを示していました。つまり、我々の計算も、CH/π相互作用やπ/π相互作用が、タンパク質の立体構造維持に重要な役割を果たしていることを示唆する結果となっています。
08
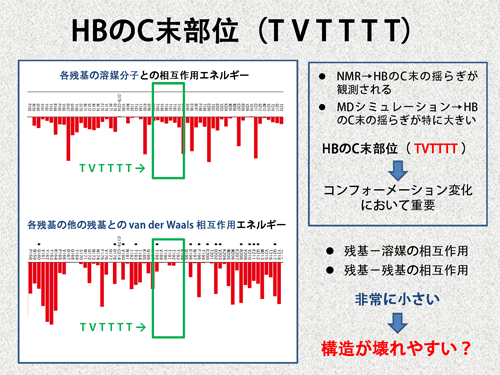
最後に、HBのC末部位に関して議論してみましょう。近年の実験や分子動力学の結果から、HBのC末部位（特に、TVTTTTのスレオニンが並ぶ部分）の揺らぎが特異的に大きい、つまり、この部分が異常型への構造変化で重要であるという内容の研究が報告されています。そこで、我々の計算結果を、このような立場から見てみることにしましょう。以下に示したのは、各残基の溶媒との相互作用エネルギーおよび他の残基と稼ぐ van der Waals 相互作用エネルギーのTVTTTT部分です。溶媒分子とも他の残基ともほとんど相互作用を及ぼしていないことが分かります。つまり、HBのC末のスレオニンが並ぶ部分は、我々の計算からも構造的に弱いと推測することができ、上の実験や分子動力学計算と矛盾しない結果だといえます。
これまでFMO法は、タンパク質−低分子化合物やタンパク質−DNAといった、生体分子の「分子間相互作用解析」に利用されて来ました。一方で、ここで紹介したような「分子内相互作用解析」に利用した例はあまり報告されていません。現在、タンパク質科学において、高次構造の形成は非常に重要で大きなテーマといえます。今後、FMO法が、そのような研究分野でも有効に利用されることを期待しています。
refrence
[1] Interaction analysis of the native structure of prion protein with quantum chemical calculations, T. Ishikawa and K. Kuwata, J. Chem. Theor. Comput., 6 (2010) 538-547 (DOI: 10.1021/ct900456v)
[2] Fragment molecular orbital method: an approximate computational method for large molecules, K. Kitaura, E. Ikeo, T. Asada, T. Nakano, and M. Uebayasi, Chem. Phys. Lett., 313 (1999) 701-706 (DOI: 10.1016/S0009-2614(99)00874-X)
[3] Fragment molecular orbital method: use of approximate electrostatic potential, T. Nakano, T. Kaminuma, T. Sato, K. Fukuzawa, Y. Akiyama, M. Uebayasi, and K. Kitaura, Chem. Phys. Lett., 351 (2002) 475-480 (DOI: 10.1016/S0009-2614(01)01416-6)